ASSOCIAZIONE CULTURALE DIEGO DE MINICIS

« Si ritiene che in qualche modo i frattali abbiano delle corrispondenze con la struttura della mente umana, è per questo che la gente li trova così familiari. Questa familiarità è ancora un mistero e più si approfondisce l'argomento più il mistero aumenta » (Benoit Mandelbrot)

Il giorno 21 Maggio 2011 il Prof. Riccardo Piergallini dell’Università di Camerino ha tenuto un seminario sui FRATTALI, presso la Sala Consiliare del Comune di Petriolo.

Il professor Piergallini ha subito informato i presenti che non avrebbe insistito sull’aspetto matematico ma che aveva impostato il seminario come una presentazione di immagini relative ai Frattali per permettere ai presenti di avere un primo contatto con l’argomento, non “traumatizzato dall’aspetto matematico”, e con la teoria del Caos.

Un frattale può essere definito come un oggetto geometrico che replica la propria struttura allo stesso modo su scale diverse (figura 5), ovvero che non cambia aspetto anche se fosse osservato per mezzo di una lente d’ingrandimento. Questa caratteristica è spesso chiamata autosimilarità. Il termine frattale è dovuto a Benoit Mandelbrot, che lo introdusse nel 1975, e deriva da fractus, così come il termine frazione; infatti le immagini frattali sono considerate dalla matematica oggetti di dimensione frazionaria. I frattali compaiono spesso nello studio dei sistemi dinamici e nella teoria del caos e sono spesso descritti in modo ricorsivo da equazioni molto semplici, scritte con l'ausilio dei numeri complessi. Ad esempio l'equazione che descrive l’insieme di Mandelbrot (Figura 4) è la seguente:

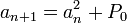
dove a_n e P₀ sono numeri complessi. Secondo Mandelbrot, le relazioni fra frattali e natura sono più profonde di quanto si creda, anzi la geometria frattale è più vicina alle immagini naturali della geometria euclidea.

Figura 1

Figura 2

Figura 3

Figura 4

Figura 5

Figura 6

Che dire del caos?

I fenomeni hanno un andamento temporale che può essere descritto da una funzione a piu' variabili. Se per semplicità usiamo una sola variabile x, il piu' semplice algoritmo che descrive l'andamento temporale di questa variabile e' come al solito una procedura ricorsiva ma questa volta in termini temporali: x(t+1) = f(x(t)). Essa è chiamata anche iterazione. Per modellare fenomeni naturali siamo interessati a iterazioni che non siano banali come quelle che fanno diventare x costante, ne' impossibili come quelle che fanno diventare x infinito. La piu' semplice iterazione non banale e' x_n+1 = r x_n(1-x_n), dove r è una costante positiva e x₀ è compresa tra 0 e 1. L'andamento di questa iterazione varia al variare del valore iniziale x₀.Il diagramma di Feigenbaum, da a colpo d'occhio l’immagine di cosa succede al variare di r. Prima x si stabilizza su un unico valore, poi tra 2, poi 4, 8,16, e infine infiniti valori, cioe' diventa caotica!

Figura 7